線形代数とは何か
ベクトル空間と線形写像の性質を研究する数学の一分野。主に行列、ベクトル、線形方程式系を扱い、科学や工学、経済学などさまざまな分野で広く応用されている。
線形(Linear)
「線形」とは、ある種の直線性を持つ性質を意味する。具体的には、関数や写像が以下の条件を満たす場合に線形と呼ばれる。
- 加法に対して閉じている:f(x+y)=f(x)+f(y)
- スカラー倍に対して閉じている:f(cx)=cf(x)
これらの性質を満たす関数や写像を線形と呼び、これを用いたモデルや方程式は線形方程式と呼ばれる。
一次関数は線形関数。一次関数の高次元バージョンが、行列による関数、線形関数。
二次関数や三角関数は非線形関数
代数(Algebra)
「代数」とは、数や量の一般化された操作を扱う数学の一分野。基本的な代数の操作には、加法、減法、乗法、除法がある。代数は数だけでなく、文字や記号を用いて数式を表現し、さまざまな法則を使って計算や操作を行う。代数の目的は、数式を操作することで解を求めたり、式の構造を理解したりすること。
線形代数では、これらの代数の概念をベクトルや行列に適用し、ベクトル空間内での操作や関係を調べる。行列を用いた計算や、ベクトル空間の基底、次元、直交性などの概念が重要な役割を果たす。
ベクトル(Vector)
- いくつかの数の組みで、大きさと方向を持つ量を表す
行列(Matrix)
- 数字を行と列に並べたもの。ベクトルも行列の一部。
- 行列の積はベクトルXを別のベクトルy=Axに変換する。行列によって、拡大縮小、反転、回転、剪断が表現できる。
線形代数の応用分野
コンピュータ科学と機械学習
- データの表現や操作、アルゴリズムの設計において行列やベクトルが広く使用される。
- 機械学習のモデル(例えば、ニューラルネットワーク)は、重み行列を用いて入力データを処理する。
物理学
- 力や運動、電場や磁場などの物理量をベクトルや行列を用いて表現する。
- 量子力学では、状態ベクトルや行列演算が重要な役割を果たす。
経済学
- 経済モデルや最適化問題の解法において、行列やベクトルを使用する。
- 例えば、入力出力分析では産業間の取引を行列表現する。
グラフィックスと画像処理
- 3Dグラフィックスのレンダリングや画像のフィルタリングにおいて、行列変換が使用される
- アフィン変換や射影変換などの幾何変換を行列で表現する。
システム工学
- 制御理論において、状態ベクトルや伝達行列を用いてシステムの動作を記述する。
- ロボティクスにおいても、ロボットの位置や姿勢をベクトルと行列で表現する。
統計学
- 多変量解析では、データを行列として扱い、主成分分析や因子分析などの手法を適用する。
- 回帰分析においても、行列演算を用いてモデルのパラメータを推定する。
連続的な問題である微分方程式を、極限まで拡大することで離散化して、数字で直線として扱うようにすることで、線形代数で解けるように単純化する
微分方程式の離散化
- 微分方程式は連続的な関数の変化を表現するが、これを有限差分法(関数の連続的な変化を、有限な差分で近似)や有限要素法(領域を小さな要素に分割し、それぞれの要素内で関数を近似する)などを用いることで、離散化することで数値的に解くことができるようになる。離散化した微分方程式は、しばしば連立一次方程式の形になるので、これを行列形式で表現し、線形代数を用いて解くことが可能になる。
行列演算の性質
- 結合法則・交換法則・分配法則は普通の数と同じ。
- 積は可換ではない(非可換):AB≠BA →普通の数と異なり、「左からかける」「右からかける」を区別する必要がある
行基本変形
文字通り、行列の行に対して行う基本的な操作のこと。これらの操作を用いることで、行列を簡単な形に変換することができ、連立一次方程式の解法や行列の階数を求める際に役立ちつ。行基本変形には次の3種類がある
- 行の交換:2つの行を入れ替える。Ri↔Rj
- 行の定数倍:ある行を0でない定数で掛ける。Ri→kRi
- 行の加減:ある行に別の行の定数倍を加える。Ri→Ri + kRj
列基本変形も行基本変形と同様に定義できるが、連立方程式の解法や行列のランク計算・逆行列の計算に不便という観点で、行基本変形が用いられることが多い。
掃き出し法(ガウスの消去法)
行基本変形を用いて行列を階段行列(上三角行列)に変換する手法。この方法は、連立一次方程式の解法や行列の階数、逆行列を求めるために用いられる。
係数行列:連立一次方程式の係数だけを取り出して行列として表現したもの
定数項ベクトル:連立一次方程式の右辺にある定数項を集めて作られるベクトル。各方程式の右辺に相当する
拡大係数行列は、係数行列に定数項ベクトルを追加して拡張した行列。これにより、連立一次方程式全体を1つの行列で表現することができる

連立方程式の解が一意に定まるか,不定の解が求まるか,解がないか(不能)は,拡大係数行列のランクと係数行列のランクに依存する。
階数(rank)と一意・不定・不能の関係
行列の階数は、行列の本質的な次元を示し、独立な方程式の数を表す。行列を行基本変形して階段行列にしたときの非ゼロ行の数。
n次元連立方程式の場合
一意解
- rank(A) = rank[A|b] かつ n = rank(A)
- 連立一次方程式の係数行列A と拡大係数行列[A∣b] のランクが一致しており、かつ、そのランクがnと一致している時
不定(解が定まらない)
- rank(A) = rank[A|b] かつ n > rank(A)
- 連立一次方程式の係数行列A と拡大係数行列[A∣b] のランクが一致しており、かつ、そのランクがnより小さい時
不能(解が存在しない)
- rank(A) ≠ rank[A|b]
- 連立一次方程式の係数行列A と拡大係数行列[A∣b] のランクが一致しない時
行列式
行列式とは、正方行列(行と列の本数が同じ行列)に対して、下記のように定義する数値。
行列Aの行列式は、det(A) または |A|と表記する。

何やらややこしいが、これを定義としたのであって覚える必要はない(私見。
上記式の右辺を理解するには、置換・互換・偶置換・奇置換の理解が必要になる。
置換と互換
置換:ある集合の要素を特定の順序で並び替える操作。
互換:置換の中でも,2つの要素を交換するだけのもの。iとjを交換する互換を(i,j)と書く。
奇置換と偶置換
置換が奇置換か偶置換かは、その置換を実行するために必要な互換の数によって決まる。
- 偶置換:偶数回の互換で表せる置換。
- 奇置換:奇数回の互換で表せる置換。
例えば、集合 {1,2,3} に対する置換 (1,3,2)は1回の互換 (2,3)で表せるので奇置換。一方、置換 (3,2,1) は2回の互換 (1,3)と(1,2)で表せるので偶置換。
置換の符号(Sign of a Permutation)は、その置換が奇置換か偶置換かを示す数値で、次のように定義される
- 偶置換の場合、符号 sgn(σ)=+1
- 奇置換の場合、符号 sgn(σ)=−1
上記定義から導き出される行列式の性質
- 転置不変性:行列の行列式は、その転置行列の行列式と等しい。det(A) = det(At)
- 交代性:行列の行や列を入れ替えると、行列式の値は-1倍される。
- 多重線形性:ある行(列)の定数倍を他の行(列)に加えても、行列式の値は変化しない。行や列ごとに足し算を分解できる。
- det(A)≠0 ⇔ Aの逆行列が存在する(Aは正則)。逆行列は正則行列を掛けると単位行列になる行列。「数aが逆数を持つこと⇔a≠0」を一般化したもの
- 2次元や3次元の空間において、行列式は平行六面体や平行四辺形の体積(または面積)を表す
- 線形変換のスケーリング:行列は線形変換を表す。行列式の値は、その変換が体積(または面積)をどの程度拡大または縮小するかを示す(符号付き)。detAが負の時は、鏡映が含まれている。
余因子展開:行列の行列式を計算する方法の一つであり、特定の要素に対応する余因子を用いる。
Mi,j は A の (i, j)小行列式、つまり、A から第i行と第j列を除いて得られる (n − 1)次小正方行列の行列式。aチルダをAの (𝑖,𝑗) (i,j) 余因子とよぶ。

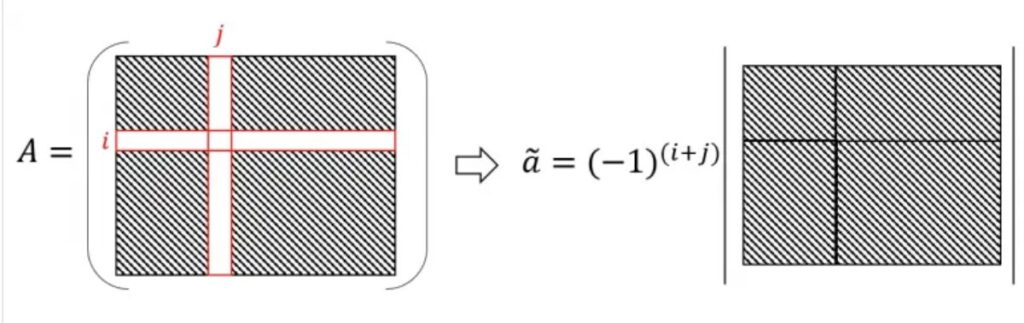
例えば、3×3の行列式の場合、余因子展開を用いることで、3つの2×2行列式の問題に落とし込むことができる。小さな行列式に分解するアイデアで、行列式のもつ多重線形性に基づいている。
行列式の定義は置換による定義で、性質としては多重線形性を持ち、実践としては余因子展開を用いるという流れ。
固有値・固有ベクトル
(定義)n次正方行列Aに対して,Ax=λx (x≠0)𝐴𝑥=𝜆𝑥 (𝑥≠0)を満たすスカラー𝜆をAの固有値,x∈Rnを𝜆に対応する固有ベクトルという.
通常ベクトルに対して、n次正方行列Aをかけるとベクトルの向きが変わるが、ある特定のベクトルの場合には、Aを作用させても向きが変わらない場合があり、そのような特別なベクトルを固有ベクトルと呼ぶ。また、その場合の長さの倍率を固有値という。
固有値と固有ベクトルの求め方
1)固有方程式の導出 固有値は次の固有方程式の解として求められる:det(A−λE)=0
Eは単位行列。上記方程式を解くことで、固有値λを求める。
2)固有ベクトルの解 固有値 λが求まったら、それに対応する固有ベクトル x は次の線形方程式を解くことで求められる。(A−λE)x=0
行列の対角化
- 与えられた正方行列Aに対して、適当な正則行列Pが存在して、P-1APを対角行列D(対角成分以外が全て0である行列)にすること。
- Aの固有ベクトルがn個の線型独立な固有ベクトルを持っている時のみ、行列の対角化が可能で、得られる対角行列の対角成分はAの固有値。。
行列Aのn乗を求めたい場合、そのまま計算すると大変なので、まず行列の対角化を行い(対角化できる場合)、対角行列Dのn乗を用いることで簡単に求めることができる。
ジョルダン標準形(準対角化)
A に固有値の重複がある場合(重解)は対角化できない場合があり、その場合は、ジョルダン標準形を用いる。
対角化できない場合でも、Aのn乗を求める場合に、できるだけ簡単に求めたいというモチベーションから生まれた。
ジョルダンブロック(ジョルダン細胞)は、対角成分に同じ値λを並べ、一つ上の部分には1を並べた行列のこと。それ以外の成分は全て0。対角成分λと行列のサイズkを用いてJ(λ,k)と書く。任意の行列Aに対してジョルダン標準形は(ブロックの順番の任意性を除いて)一意に決まる。


