はじめに
アインシュタインの相対性理論は興味はあったものの、今まで読んだことはなかったので、まずは超入門の読み物の本を読了。中学・高校物理レベルを理解していれば、理解できるくらいに噛み砕かれて説明されていた。
詳しく正確に理解するためには大学レベルの物理が必要だろうが、概略を理解したかった自分としてはとても参考になる本だった。
以下、印象に残った部分を備忘録的に記載。
ニュートン→マクスウェル→アインシュタインという法則統一の過程
物理学の発展は、多種多様な法則を統一する歩みであったとも言える。
ニュートン:運動の法則を統一
ガリレオやケプラーの成果を統合
- ニュートンは運動の法則を統一し、質量保存・運動量保存・エネルギー保存といった法則を「万有引力」の理論にまとめた。
絶対空間の概念
- 物体は空間内で運動・変化するが、空間自体は永久不変とする考え方。→ この絶対空間の考えは後に相対性理論によって覆されることになる。
マクスウェル:電気と磁気の法則を電磁気学として統一
電気と磁気の統合
- 電気と磁気を一体化した理論を構築。例:電磁波は電場と磁場が交互に生成しながら光速で伝わる。
光の本質を解明
- 光も電磁波の一種であり、電場と磁場の相互作用によって伝わる現象であることを示した。
アインシュタイン:時空間の統一・質量とエネルギーの統一
- 特殊相対性理論:運動の法則(ニュートン力学)と電磁気学(マクスウェルの方程式)を統一し、光速不変の原理に基づいた新たな運動の理論を構築。
- 一般相対性理論:時間と空間を時空として統一し、重力を時空の幾何学的な歪みとして解釈
- 結果として、ニュートン力学で表されていた、質量保存・運動量保存・エネルギー保存の法則が、エネルギー運動量保存という1本の方程式にまとめ上げられることになった。
特殊相対性理論と一般相対性理論の概要
特殊相対性理論:慣性系の中で成り立つ理論
光速度不変の原理:光の速さ c は観測者の運動速度にかかわらず常に一定。
ニュートン力学では、速度は観測者の運動状態によって異なる(相対速度の加算法則が成り立つ)とされていたが、実験結果から観測者の運動状態によって光の速度は変わらないことが示された。
アインシュタインは上記のニュートン力学とマクスウェル電磁気学の矛盾を解決するために、「観測者が等速直線運動している限り、光の速度はその運動状態(速度)にかかわらず一定」という原理を仮定し、相対性原理を導入し、それを元に時間も空間も相対的なものであることを示した。
- 時間と空間の相対性:時間は絶対ではなく、運動している観測者の速度に応じて伸びたり縮んだりする(時間の遅れ)。空間の長さも観測者に応じて変化する(長さの収縮)。
- 質量とエネルギーの関係:有名な式 E=mc2 によって、質量とエネルギーが等価であることを示した(光速度不変の原理と質量保存・運動量保存の法則から導かれる)。これにより、核融合や核分裂のエネルギー生成メカニズムを説明可能に。
一般相対性理論:重力を含むあらゆる系で成り立つ理論
- 重力=時空の歪み:質量のある物体は周囲の時空を歪め、その歪みが他の物体の運動に影響を与える。これが重力の本質。
- 光も重力の影響を受ける:光も時空の歪みによって進路が曲がる(重力レンズ効果)。
- 自由落下と等価原理:重力場での自由落下は慣性系と区別がつかない、という原理に基づいて理論を構築。
非慣性系や重力場の影響下では、観測者の運動状態や空間の性質が変わるため、光の進む道筋が曲がって見える場合がある。ただし、光速度は一定。この現象を説明するために、アインシュタインの一般相対性理論では、重力は「空間(時空)」そのものの歪みとして説明した。
光は慣性系によって歪んだ空間(時空)を「最短経路」で進もうとするため、結果的に曲線的な進路を取ることになる。
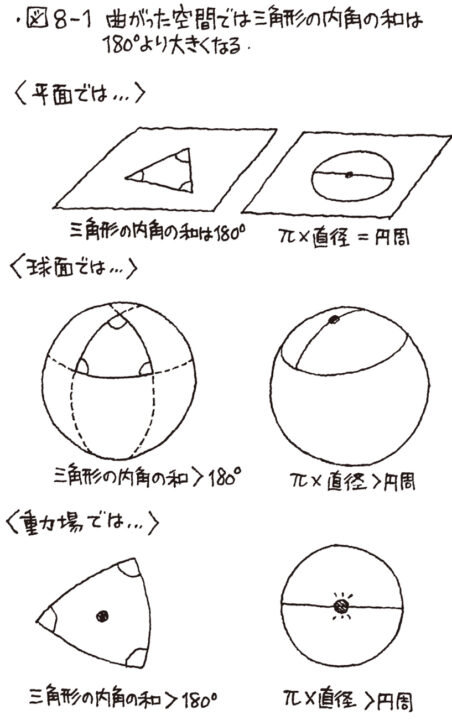
光が曲がるのは、空間そのものが歪んでいるためであり、光はその歪んだ空間の中で可能な限り最短の経路を進んでいるだけと捉え直したところに新規性がある。
E=mc² :質量がエネルギーに変換可能であることを示す式
エネルギーと質量の等価性:質量 m が完全にエネルギーに変換された場合のエネルギー量 E を表す。
相対性原理とエネルギーの関係
アインシュタインは特殊相対性理論を通じて、以下の2つの重要な事実を導いた
運動エネルギーと静止エネルギー
- 古典力学では、エネルギーは「運動エネルギー:K=1/2mv2」に限られていた。運動エネルギーは質量に比例し、運動速度の2乗に比例するというもの。この古典的な運動エネルギーの式は、低速(光速に比べて非常に遅い速度)では正確に適用されるが、速度が光速に近づく場合には特殊相対性理論の補正が必要になる。
- しかし、相対性理論では、運動していない物体にもエネルギーがあることが示された。このエネルギーが「静止エネルギー」であり、その式が E=mc2 。
感覚的には運動している物質はエネルギーを持っていそうだが、静止している物質もエネルギーを持っているなんて信じられないが、実際には質量はエネルギーが凝縮した形として存在している。
ただ、静止エネルギー E=mc2を実際に活用するためには、質量欠損を引き起こすような物理的なプロセスが必要にな理、そのためには非常に大きなエネルギーが必要になる。そのため、ため、私たちは日常生活の中で静止エネルギーの存在を、運動エネルギーや位置エネルギーなどのように直接実感することがほとんどないので、実感が湧きづらいとも言える。
質量とエネルギーの等価性
- 相対性理論では、物体の質量 m とエネルギー E が本質的に同じものであると示された。この「質量エネルギー等価性」が核反応や宇宙物理学でのエネルギー生成を説明できるようになった。
- 日常生活への影響:原子力発電や核兵器の原理がこの式に基づいている。
例えば、太陽の中心では 、4つの水素原子核(陽子) が融合して、1つのヘリウム原子核 が作られるが、この過程で、反応前後の質量に差(質量欠損)が生じる。この欠損した質量がE=mc2によってエネルギーに変換される。
電磁力と重力の比較:スケールの違い
- 電磁力:電荷の間に働く力で、重力に比べ非常に強い。静電気の力で髪の毛を持ち上げるほど簡単に観測可能。
- 重力:質量を持つ物体間に働く力。ただし、非常に弱い。地球規模の質量が集まってようやく観測可能な重力場を形成。
- 重力波:質量が加速運動することで、周囲の時空の歪みが光速で伝播する現象。ブラックホール同士の衝突など非常に強い重力場の変動によって生じ、地球上の観測機器(LIGOなど)で捉えることができる。
場の理論:直接相互作用から場を介した相互作用へ
ニュートン力学では、物体同士が「直接」力を及ぼし合うように見えたが、マクスウェルやアインシュタインの理論では、力は場を介して伝わると考える。
| 従来の直接相互作用モデル | 場の理論によるモデル |
| 物体同士が直接作用する | 物体は場を介して相互作用 |
| 力の伝達機構は不明 | 場が力の伝達機構を説明 |
| 重力や電磁力の遠隔作用を説明できない | 遠隔作用を場で説明可能 |
場の概念は量子力学にも取り入れられ、「量子場理論」 として統一的な枠組みが構築された。電磁場や重力場だけでなく、物質の基本粒子(電子やクォーク)も場として記述される。
人間関係のアナロジーでいくと、人間(物質)の行動が職場や家庭などの「環境」を変化させ、変化した環境によって他の人の行動や性格が変わっていくような感じ。例えば、ストレスの多い職場では、そこにいる人たちの行動やパフォーマンスが変わるような。
相対性理論がもたらした新たな視点
アインシュタインの理論は、物理学の枠組みを大きく変え、以下のような新たな視点を与えた
- 時間と空間は絶対ではなく、観測者や状況に応じて変化する。
- 重力は単なる「力」ではなく、時空そのものの性質。
- エネルギーと質量は本質的に同じものであり、宇宙のエネルギー循環に深く関与している。
このような理論的革新は、ブラックホールや宇宙の膨張など、現代物理学の多くの分野に応用されている




